Convolutional neural networks or CNNs are deep neural networks considered as the most representative model of deep learning. CNNs extend on traditional neural networks by combining both fully-connected hidden layers and locally-connected convolutional layers. In traditional neural networks, each neuron in the hidden layer is fully-connected to all neurons in the preceding layer. However, in case of large 2D input images full-connectivity gets highly computationally expensive. It also does not take advantage of the local correlations of pixels in real-world images. Inspired by the biology of human vision, CNNs take advantage of the spatial correlation of objects present in real-world images and restrict the connectivity of each node to a local area known as its receptive field. According to LeCun, Bengio and Hinton in Deep Learning (Nature 2015), CNNs use four key ideas that greatly reduce the number of parameters to be learned and improve the approximation accuracy compared to traditional DNNs. These are: local connections, shared weights, pooling and the efficient use of many layers.
Basic Architecture
A typical CNN architecture is demonstrated in Fig. 1.
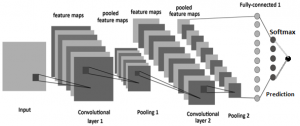
The hidden layers in a CNN can be any of the three types from convolutional layer, pooling layer and fully-connected layer. Each neuron in the input layer takes each image pixel as input variables and passes them to a small number of adjacent neurons of the next layer they are connected to. Image region covered by these adjacent neurons is called the receptive field as mentioned earlier. Each neuron in the hidden layer takes a receptive field from the previous layer as input and transforms that into many different representations by applying convolution and pooling filters. Filters are 2D matrices of weights which are analogous to the weight parameters of the traditional DNN described in previous section. For each filter, a different representation of the output of previous layer is obtained which is called a feature map. In Fig. 1, stacked images in the convolutional and pooling layers are the feature maps or channels or layer depths. Filter weights are shared across a single feature map. On the other hand, different shared filter weights are used for different feature maps. Activation functions are applied to each of the feature maps individually in each layer.
Convolution
Convolutional filters convolute a weight matrix with the values of a receptive field of neurons in order to extract useful features or patterns. These filters learn more high- level features as the network gets deeper. At the beginning of the training, weights are randomly initialized. However, during training process, weights are adjusted through backpropagation in order to learn the features which are most representative for correct prediction.
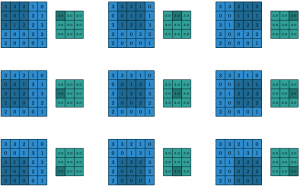
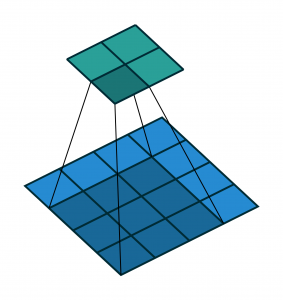
In Fig. 2, an input matrix in light blue is convolved by a filter matrix in dark blue and generates a feature map in green by taking the summation of the element- wise product of each cell of the filter and each cell of the area covered by the filter of the input matrix. In this convolution, no zero-padding on the input matrix and stride of 1 on the filter is used.
Pooling
Although the role of the convolutional layer is to detect local conjunctions of features from the previous layer, the role of the pooling layer is to merge semantically similar features into one. In other words, pooling layers compress the responses of a receptive field into a singleton value to produce more robust feature representations. A typical neuron in the pooling layer (MaxPool) takes the maximum of a local patch or region of cells in a feature map resulting in a lower dimensional representation of the particular feature map. As a result, locally connected pooling neurons take features from patches that are already shifted by more than one row or column, thereby creating an invariance to small shifts and distortions to new unseen images.
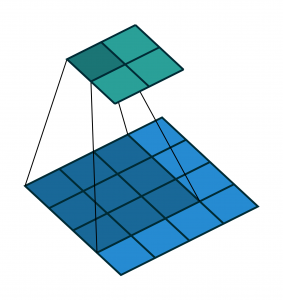
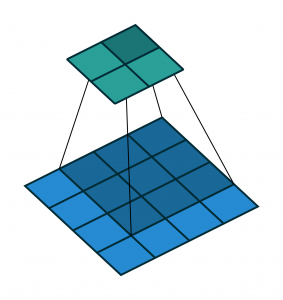
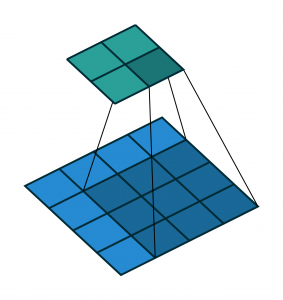
In Fig. 3, a 5 × 5 feature map is reduced to a 3 × 3 map after taking the maximum value from each of the nine patches using 1 x 1 strides. Pooling filter weights are not learnable parameters thus they don’t take part in backpropagation.
CNN as Feature Extractor
CNNs have the great advantage of very deep feature extraction through hierarchical representation of images from pixel to high-level semantic features. In CNNs, features extracted from one convolution layer followed by a pooling layer are passed as input to next layer along with all the different transformation learned by feature maps. More importantly, CNNs learn this representation automatically from the given data without any domain-expert defined rules. Along with multi-layer non- linear mappings using activations, many hidden pattern of the input data can also be discovered which makes CNNs exponentially expressive compared to traditional computer vision algorithms. Therefore, currently CNNs are the most common model to be used as the base feature extractor in any computer vision tasks including image classification, object detection, face recognition etc.
I hope you have found this article useful. Please feel free to comment below about any questions, concerns or doubts you have. Also, your feedback on how to improve this blog and its contents will be highly appreciated. I would really appreciate you could cite this website should you like to reproduce or distribute this article in whole or part in any form.
You can learn of new articles and scripts published on this site by subscribing to this RSS feed.
Like!! Really appreciate you sharing this blog post.Really thank you! Keep writing.
“I think this site has got some really wonderful info for everyone :D. “We rarely think people have good sense unless they agree with us.” by Francois de La Rochefoucauld.”
Hi Werner, thanks for your kind words! Glad that it helped you.
“This site was… how do you say it? Relevant!! Finally I’ve found something that helped me. Cheers!”
Hi Luna, thanks for your kind words! Glad that it helped you.
Pretty great post. I simply stumbled upon your blog and wanted to mention that I’ve really loved surfing around your weblog posts. After all I’ll be subscribing for your feed and I hope you write again very soon!| а
Thanks so much for your kind words! I got busy with other stuffs. But your words have inspired me to be regular again!